堆

堆就是用数组实现的二叉树，所以它没有使用父指针或者子指针。堆根据“堆属性”来排序，“堆属性”决定了树中节点的位置。 堆（英语：Heap）是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。

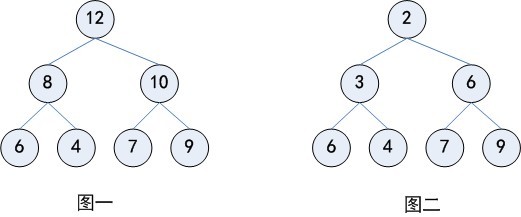
堆也被称为优先队列（priority queue），队列中允许的操作是先进先出（FIFO），在队尾插入元素，在队头取出元素。而堆也是一样，在堆底插入元素，在堆顶取出元素，但是堆中元素的排列不是按照到来的先后顺序，而是按照一定的优先顺序排列的。这个优先顺序可以是元素的大小或者其他规则。如图一所示就是一个堆，堆优先顺序就是大的元素排在前面，小的元素排在后面，这样得到的堆称为最大堆。最大堆中堆顶的元素是整个堆中最大的，并且每一个分支也可以看成一个最大堆。同样的，我们可以定义最小堆，如图二所示。

堆的常用方法：

• 构建优先队列
• 支持堆排序
• 快速找出一个集合中的最小值（或者最大值）

堆和二叉搜索树的区别

• 节点的顺序。在二叉搜索树中，左子节点必须比父节点小，右子节点必须必比父节点大。但是在堆中并非如此。在最大堆中两个子节点都必须比父节点小，而在最小堆中，它们都必须比父节点大。
• 内存占用。普通树占用的内存空间比它们存储的数据要多。你必须为节点对象以及左/右子节点指针分配内存。堆仅仅使用一个数据来存储数组，且不使用指针。
• 平衡。二叉搜索树必须是“平衡”的情况下，其大部分操作的复杂度才能达到O(log n)。你可以按任意顺序位置插入/删除数据，或者使用 AVL 树或者红黑树，但是在堆中实际上不需要整棵树都是有序的。我们只需要满足堆属性即可，所以在堆中平衡不是问题。因为堆中数据的组织方式可以保证O(log n) 的性能。
• 搜索。在二叉树中搜索会很快，但是在堆中搜索会很慢。在堆中搜索不是第一优先级，因为使用堆的目的是将最大（或者最小）的节点放在最前面，从而快速的进行相关插入、删除操作。

存储

要实现一个堆，我们可以先思考，如何存储一个堆。 树的存储方式一般有链式存储和线性存储，分别对应我们常见的链表和数组两种方式，对于完全二叉树而言，用数组来存储是非常节省存储空间的，因为不需要存储左右子节点的指针，单纯地通过数组的下标，就可以找到一个节点的左右子节点和父节点， 所以堆我们一般也用数组来存储， 为什么我们要从数组下标 1 开始存储，从 0 开始不行吗？ 当然可以，如果从 0 开始存储，在代码的实现上，只是计算子节点和父节点的下标的公式改变了，对于下标为 i 的任意节点，

int leftIndex = 2 * i;
int rightIndex = 2 * i + 1;
int parentIndex = i / 2;

那为什么我们不从下标 0 开始存储呢？我想你应该已经猜到答案了，这里与 数组下标从 0 开始计数，而不是 1 开始 有着异曲同工之妙，我们从下标 1 开始存储，每次计算子节点和父节点时，都可以减少一次加法操作，本质是为了提高代码的性能。 知道了如何存储一个堆后，我们接着来看堆都支持哪些操作？ 一般来说，堆有几个核心的操作，比如往堆中插入一个元素，删除堆顶元素。

堆的构建

考虑这么一个问题，从一个空的堆开始，插入 n 个元素，不在乎顺序。

直接一个一个插入需要 O(n \log n) 的时间，有没有更好的方法？

方法一：使用 decreasekey（即，向上调整） 从根开始，按 BFS 序进行。

void build_heap_1() {
  for (i = 1; i <= n; i++) up(i);
}

为啥这么做：对于第 k 层的结点，向上调整的复杂度为 $O(k)$ 而不是 $O(\log n)$。

总复杂度：$\log 1 + \log 2 + \cdots + \log n = \Theta(n \log n)$。

（在「基于比较的排序」中证明过）

方法二：使用向下调整 这时换一种思路，从叶子开始，逐个向下调整

void build_heap_2() {
  for (i = n; i >= 1; i--) down(i);
}

换一种理解方法，每次「合并」两个已经调整好的堆，这说明了正确性。

注意到向下调整的复杂度，为 $O(\log n - k)$，另外注意到叶节点无需调整，因此可从序列约 n/2 的位置开始调整，可减少部分常数但不影响复杂度。

操作

接下来使用最小堆来进行操作，基本操作定义如下：

MinBinaryHeap()：创建一个空的二叉堆对象 min_insert(self,data)：将新元素加入到堆中 remove(self,data)：删除堆中某个元素 minChild(self, i)：返回子树中最小的索引值 buildHeap(list)：从一个包含节点的列表里创建新堆

堆的插入

往堆中插入一个元素后，为了保持堆的特性，我们需要对插入元素的位置进行调整，这个过程叫做堆化（heapify），以最大堆为例，

插入操作 插入操作是指向二叉堆中插入一个元素，要保证插入后也是一棵完全二叉树。

最简单的方法就是，最下一层最右边的叶子之后插入。

如果最下一层已满，就新增一层。

插入之后可能会不满足堆性质？

向上调整：如果这个结点的权值大于它父亲的权值，就交换，重复此过程直到不满足或者到根。

可以证明，插入之后向上调整后，没有其他结点会不满足堆性质。

向上调整的时间复杂度是 $O(\log n)$ 的。

堆的删除

堆中数据的删除我们可以先考虑删除堆顶元素。 从堆定义的第二条我们发现，堆顶元素存储的就是堆中数据的最大值或者最小值，以最大堆为例，最容易想到的是：删除堆顶元素后，把子节点中较大的元素放到堆顶，然后迭代地删除第二大节点，以此类推直到叶子节点被删除，

删除操作指删除堆中最大的元素，即删除根结点。

但是如果直接删除，则变成了两个堆，难以处理。

所以不妨考虑插入操作的逆过程，设法将根结点移到最后一个结点，然后直接删掉。

然而实际上不好做，我们通常采用的方法是，把根结点和最后一个结点直接交换。

于是直接删掉（在最后一个结点处的）根结点，但是新的根结点可能不满足堆性质……

向下调整：在该结点的儿子中，找一个最大的，与该结点交换，重复此过程直到底层。

可以证明，删除并向下调整后，没有其他结点不满足堆性质。

时间复杂度 $O(\log n)$。

实现

不用stl

void swap(const int &x,const int &y){
  if (x >= heap.size() || y >= heap.size()) return;
  int temp = heap[x];
  heap[x] = heap[y];
  heap[y] = temp;
}

void sink(int x) {
  while (x > 1 && heap[x] > heap[x / 2]) {// 如果x不是第一个，且大于它的父节点， 交换它和父节点并指向上一个。
    swap(x, x / 2);
    x /= 2;
  }
}

void rise(int x) {
  int next;
  while (x * 2 <= heap.size() - 1) { //如果x存在左孩子
    next = x * 2; //交换指针指向左孩子
    if (next + 1 <= n && heap[next + 1] > heap[next]) ++next; //如果右孩子存在且右孩子比左孩子大，指向右孩子
    if (heap[next] <= heap[x]) break; // 比较该指针和交换指针的大小，如果到底，则跳出循环
    swap(x,next); // 否则搅浑
    x = next;
  }
}